Parábolas

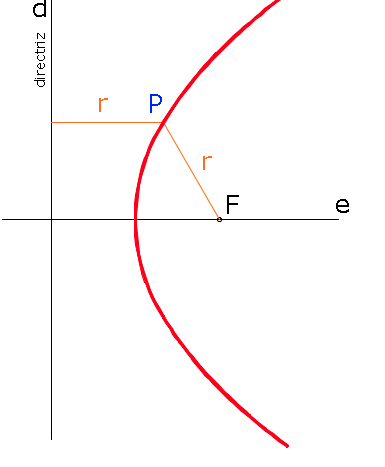
La parábola es una curva plana, abierta y de una rama. Se define como el lugar geométrico de los puntos del plano que equidistan de un punto fijo F llamado foco, y de una recta fija d llamada directriz

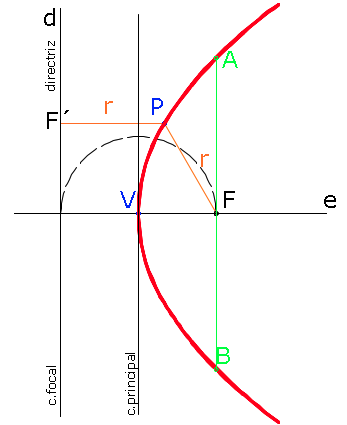
Propiedades:

1. La parábola tiene un eje perpendicular a la directriz.
   
2. La parábola tiene un vértice V y un foco F situados en el eje. El vértice, como cualquier otro punto de la parábola, equidista de la directriz y el foco.
3. Simetría: la parábola es simétrica respecto del eje.
   
4. Radios vectores: son las rectas PF y PF´ que unen un punto con el foco y con la directriz.
   
5. Circunferencia principal: es la recta tangente en el vértice; por tanto tiene radio infinito.
   
6. Circunferencia focal: es la propia directriz; por tanto tiene radio infinito
   

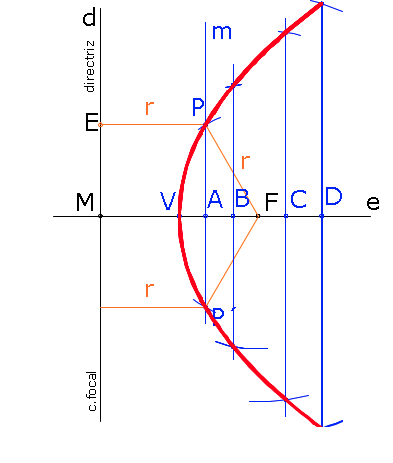
Construcción de la parábola conociendo el foco y la directriz:

1. El vértice es el punto medio del segmento MF.
   
2. Se toma un punto cualquiera A del eje y se traza la recta m perpendicular al eje.
   
3. Con centro en el foco F y radio AM se traza un arco que corta a la perpendicular m en los puntos P y P´, puntos de la parábola. Se cumple que PF = PE