Parábola

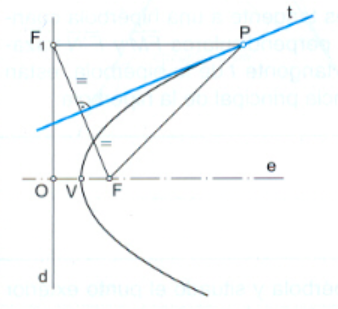
Trazado de rectas tangentes a una parábola mediante la recta directriz:

La recta directriz de una parábola es la recya perpendicular al eje e que pasa por el punto O y que equivale a la circunferencia loca de la parábola, pero de radio finito.

La recta directriz es el lugar geométrico que ocupan los puntos simétricos del foco respecto de las tangencias a la parábola.

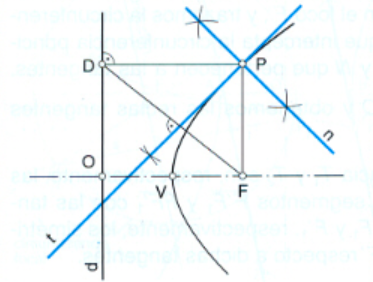
Trazado de recta tangente t y la recto normal n por un punto de la parábola:

Una vez construida la parábola y situado el punto P por el que queremos trazar la recta tangente; se une el punto P con el foco F y se traza una perpendicular a la recta directriz d por P, con lo que se determina el punto D.

• La recta tangente, t, a la parábola por un punto P de ella es la bisectriz del ángulo formado por los segmentos PF y PD.
• La recta normal, n, a la parábola por un punto P de ella es la perpendicular a la recta tangente t que pasa por dicho punto.