Arco capaz y división de segmentos

Arco capaz

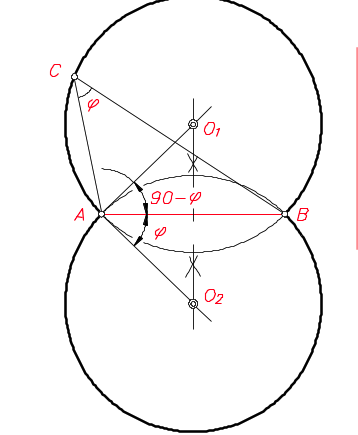
Pasos para realizar un arco capaz:

Definición: lugar geométrico de los puntos desde los cuales se ve un segmento bajo un ángulo dado

1. Se traza la mediatriz del segmento AB            
2. Por A se traza un ángulo 90-ϕ                         
3. Se halla el punto simétrico de O1                    
4. Los puntos O1 y O2 son los centros de los arcos capaces
   

División de un segmento en partes iguales

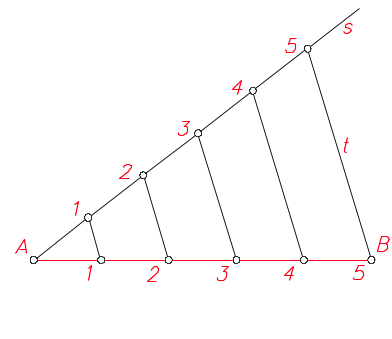
Pasos para dividir un segmento en partes iguales:

1. Por uno de los extremos A se traza una recta cualquiera s                                                         
2. Sobre la recta s se llevan tantos segmentos iguales, de longitud arbitraria, como número de partes se quiera dividir el segmento.                    
3. Se traza la recta t uniendo el último punto con el extremo B del segmento dado.                       
4. Se trazan paralelas a t por los puntos 1, 2, 3, ... de la recta s.

División de un segmento en partes proporcionales

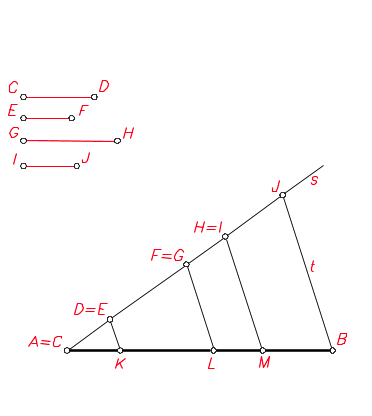
Pasos para dividir un segmento en partes proporcionales:

1.  Por uno de los extremos A se traza una recta cualquiera s.                                                            
2. Sobre la recta s se van llevando cada uno de los segmentos CD, EF, GH e IJ                              
3. Se une el último punto J con el otro extremo B mediante la recta t.                                              
4. Se trazan paralelas a t por los puntos E, G e I